
Lo scopo della seguente trattazione è quello di dimostrare, mediante l'uso degli integrali di superficie, l'equivalenza della carta di Peters e la non-equivalenza della carta di Mercatore. Il lettore non voglia vedere in tutto ciò alcuna presa di posizione dell'autore riguardo i dibattiti geo-politico-economico-sociali che traggono spesso spunto dal confronto fra le due modalità di rappresentazione del pianeta.
- Nella seguente trattazione, considereremo la terra come una sfera perfetta - Senza perdere di generalita', considereremo proiezioni centrate in latitudine rispetto all'equatore, inteso in senso geografico, per facilitare la comprensione al lettore - D'ora in poi, indichiamo con R il raggio terrestre (assunto costante per il punto 1) - In prima analisi, calcoliamo l'estensione superficiale di una porzione di superficie sferica; successivamente confrontiamo tale risultato con l'area della corrispondente porzione di superficie ottenuta per proiezione cartografica - Il lettore si aiuti con alcuni semplici disegni
Vogliamo calcolare l'area di una porzione di superficie sferica, da confrontare poi con l'estensione della omologa superficie ottenuta per proiezione cartografica. Immaginiamo di porre un sistema di assi cartesiani (xyz) nel centro della sfera, con l'asse z lungo l'asse terrestre. Esprimiamo le coordinate dei punti della superficie sferica con le coordinate sferiche (polari):
x= R sen(a) cos(b) y= R sen(a) sen(b) z= R cos(a)
in cui a rappresenta l'angolo di latitudine misurato a partire dall'asse z (ovvero 0° al polo N, 90° all'equatore, 180° al polo S) ; b l'angolo di longitudine. Osserviamo che una porzione di superficie sara' compresa fra due valori di latitudine e due di longitudine; un intero "spicchio" di sfera sara' compreso fra due valori di longitudine e latitudine da 0 a 180° ; una "fascia" longitudinale avra' b compreso fra 0 e 360°, a compreso fra due valori a1 e a2. A questo punto possiamo procedere con il calcolo dell'area compresa fra i valori A1 e A2 per a, B1 e B2 per b. Area(s) :

Area(s)= R^2 (B2 - B1) ( cos(A1) - cos(A2) )
La proiezione di Peters consiste in una proiezione cilindrica, ovvero effettuata sulla superficie di un cilindro tangente alla terra (per semplicita', tangente all'equatore), con raggi perpendicolari all'asse del cilindro (e della terra stessa). In altre parole, si puo' immaginare la terra "avvolta" da un cilindro e "affettata" con piani paralleli al piano equatoriale. Immaginiamo di porre un sistema di assi cartesiani (xyz) nel centro della sfera, con l'asse z lungo l'asse terrestre. La proiezione in esame non fa variare la quota z dei punti della superficie terrestre, mentre i valori delle coordinate x e y vengono "traslati" dalla superficie della sfera a quella del cilindro. La condizione necessaria affinche' un punto (xyz) appartenga alla superficie del cilindro e' espressa da x^2 + y^2 = R^2 . Esprimiamo ora le coordinate dei punti proiettati sul cilindro con coordinate cilindriche:
x= R cos(b) y= R sen(b) z= z
(b e' definito come al punto 1). Ora dobbiamo individuare gli estremi della superficie proiettata dalla sfera al cilindro. Come osservato in precedenza, la coordinata z rimane invariata nella proiezione. Se la regione di superficie sferica (cfr punto 1 ) era delimitata dagli angoli di latitudine A1 e A2, la coordinata z sulla superficie cilindrica sara' limitata dai valori R cos(A1) e R cos(A2). Per quanto riguarda l'angolo b, appare evidente con un semplice disegno che rimane limitato fra B1 e B2 (come al punto 1). Non ci resta che integrare! Area(s') =

La proiezione di Mercatore è una proiezione cilindrica come la precedente, ma viene effettuata tramite raggi proiettanti uscenti dal centro della sfera. Mediante un semplice disegno si intuisce che, a differenza del caso precendente, la coordinata z dei punti del cilindro puo' variare fra i valori limite di R cotan(A1) e R cotan(A2). Il valore dell'angolo di longitudine b, invece, rimane compreso fra B1 e B2. Otteniamo il seguente integrale:

Area(s'')= R^2 (B2 - B1) ( cotan(A2) - cotan(A1) )
Confrontando i risultati si nota la diversa dipendenza dal valore degli angoli di latitudine. In particolare, per angoli vicini a 0 o a 180° (cioe' in prossimita' dei poli) il valore delle aree esplode. Solo nei pressi dell'equatore la proiezione mantiene l'equivalenza (come mostra il grafico). 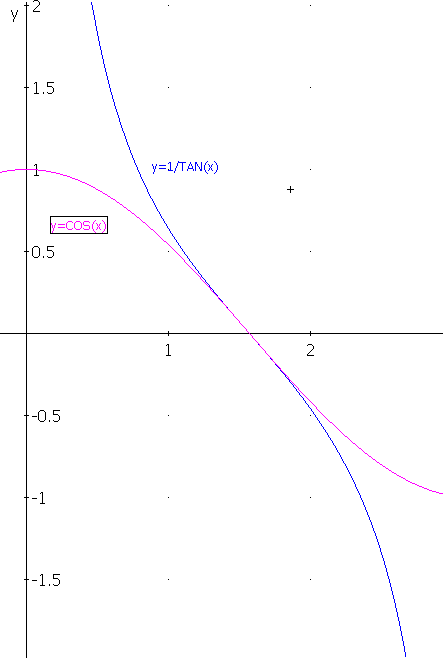
Realizzato da Federico Fontana Ultima modifica: 19/12/2009 Per chiarimenti, suggerimenti e simili: fex.1989@yahoo.it